In the previous articles in this series, I have written about what network analysis is and how to organize your database. Today’s article is about important decisions that you have to make when studying networks: I will discuss two- and one-mode networks, weighted versus binary networks, and directed versus undirected networks.
Two-mode networks
Two-mode networks, also called bimodal or bipartite networks, demonstrate how two sets of elements are connected, as for example a group of sites and the types of stone vessels excavated at these sites. The graph that illustrates this network will then look like the following.
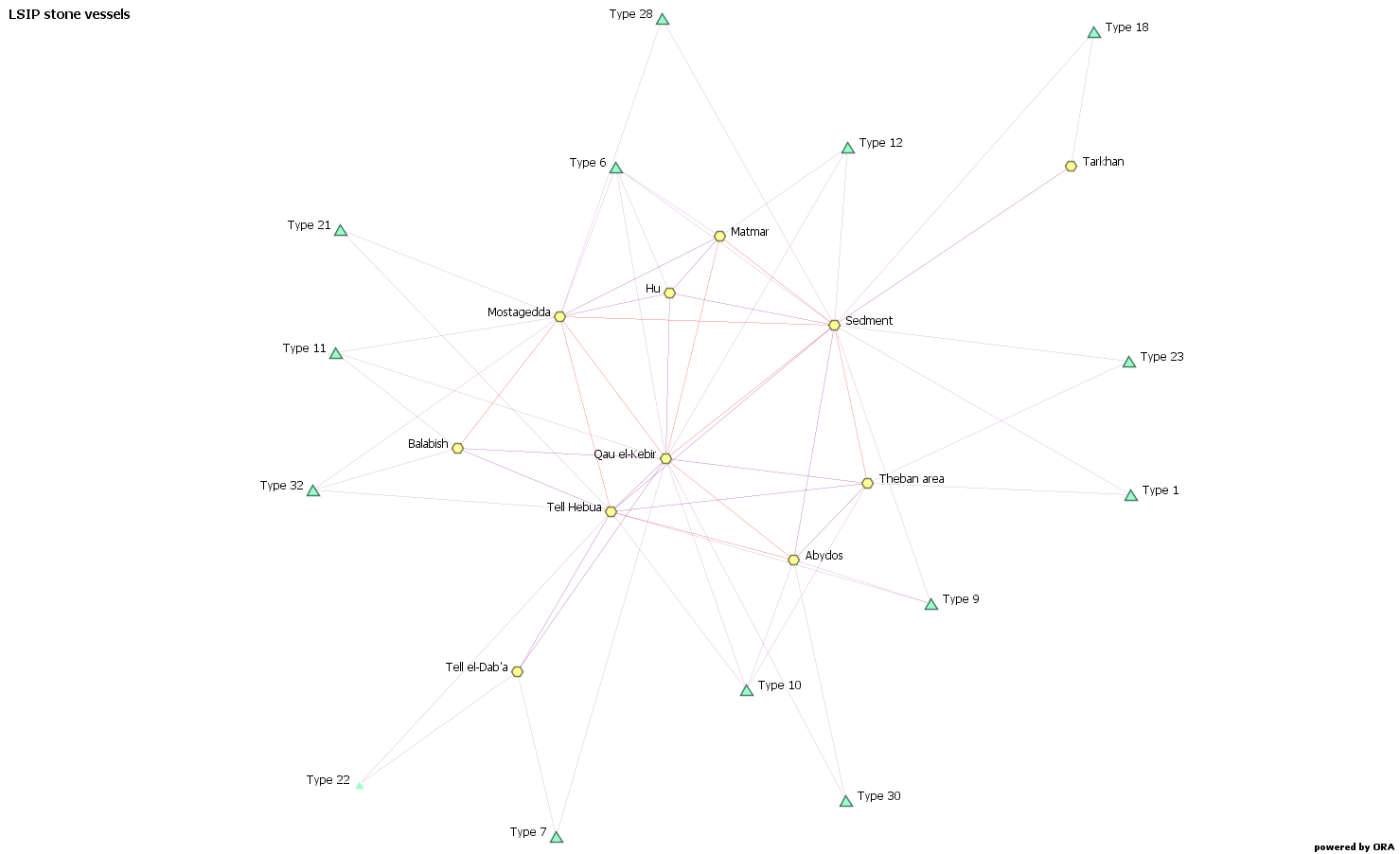
The graph here represents both the stone vessels (triangles) and the sites (hexagons), showing how the two are linked to each other. There are no connections between the different types of stone vessels; only between types of stone vessels and sites, as well as between sites. I will talk in detail about the graphs and how to visualize the networks in a future article.
Weighted versus binary networks
For now, I will focus on one of the decisions you have to make before you create a matrix and import it into the program that affects the network and the graph. As written about in the previous article, you need to decide if the links are based on a specific amount (e.g. of objects or contexts) or only on the presence/absence of a particular element shared.
In the example here, you need to decide if the links represent how many stone vessels of each type are at each site, or if they represent from how many contexts each type of stone vessel comes from, or if they represent simply the presence/absence of each type at each site.
The difference between the first two options and the third is that with the first two you will get a “weighted” network, where the links are based on the amount of what is shared (in our case of stone vessels or of contexts). In this case, the links become stronger or weaker if the amount of the elements shared grows or decreases, corresponding to thicker or thinner lines in the graph.
In the last case, you will get a binary network, where the links indicate only the presence/absence of the objects in question, making no difference as far as the strengths of the links involved (in our case: how often the types of stone vessels are found).
This decision has to be made beforehand and depends on how you compile the matrix that you “feed” into the software. However, you can still make some modifications when you import the matrix into the software, or even when you visualize the network, but I will discuss these issues in the next article.
All in all, a weighted network focuses on how often, in this example, the different types of stone vessels are found at sites, while a binary network does not. Even though a weighted network can provide more depth to the analysis, what to opt for really depends on how detailed your data is and how big your sample is. If the data available isn’t representative enough, a weighted network can lead to an overinterpretation of the results and generate a distorted image.
In my own research, for the two-mode network (vessels and sites), I did not consider my data detailed enough to choose the weighted option, because often I did not know the exact number of contexts or vessels. Moreover, considering the number of stone vessels or of contexts would mean that I considered my sample more or less complete, or at least that the sites had been all excavated and published to a comparable extent. However, this was not the case. The results would have suggested a site was more or less important based primarily on the state of its excavation.
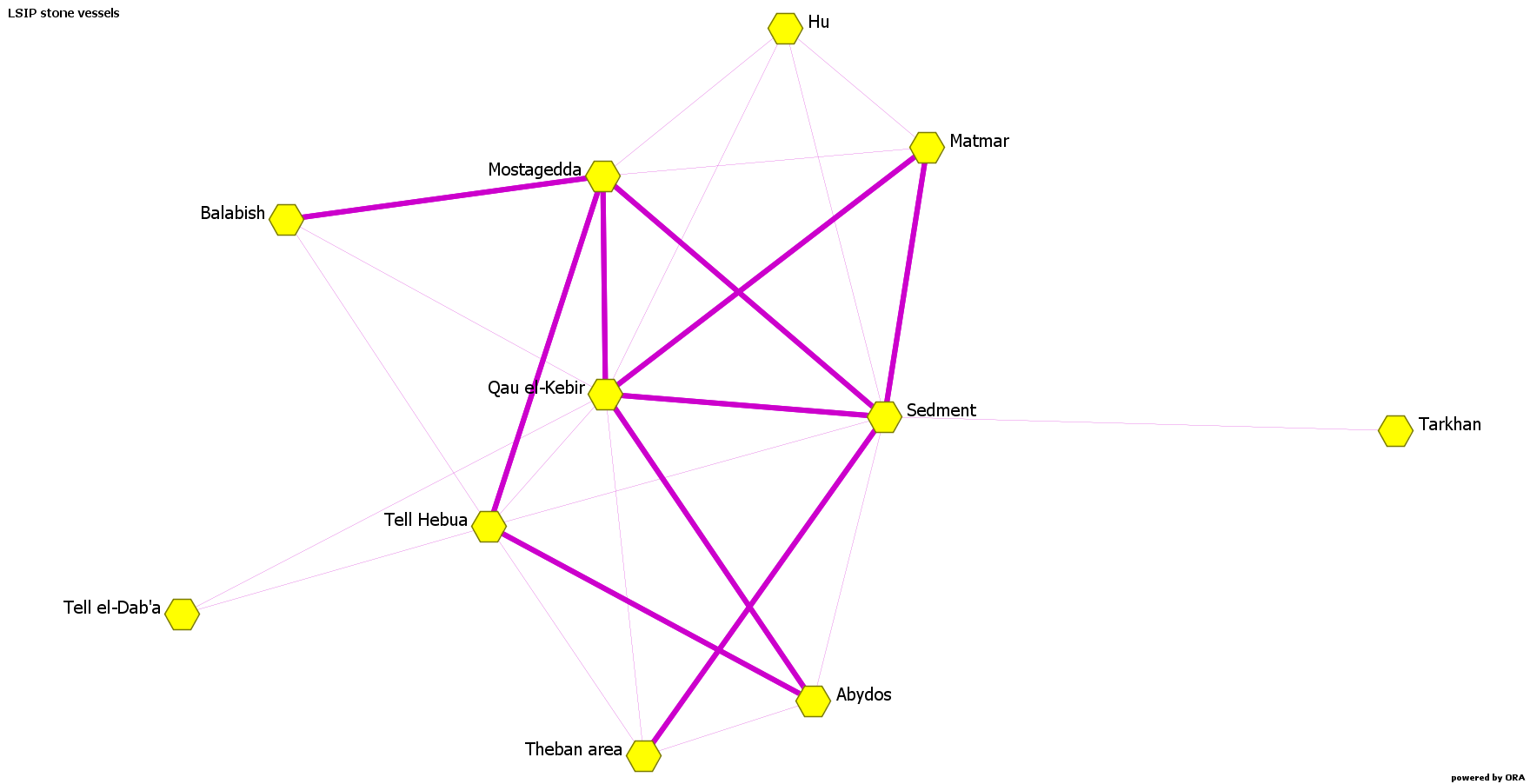
It should be noted that a bimodal network can become a one-mode network. A one-mode network shows the connections only among one set of elements. Going back to our example, a one-mode network shows only how the sites or how the stone vessels are connected. In the first case, the network looks like the following, where the hexagons represent the sites, and the links show how many types of stone vessels they have in common.
In the second case, the network looks like the following, where the triangles represent the types of stone vessels, and the links show at how many sites these types of objects have been found together.
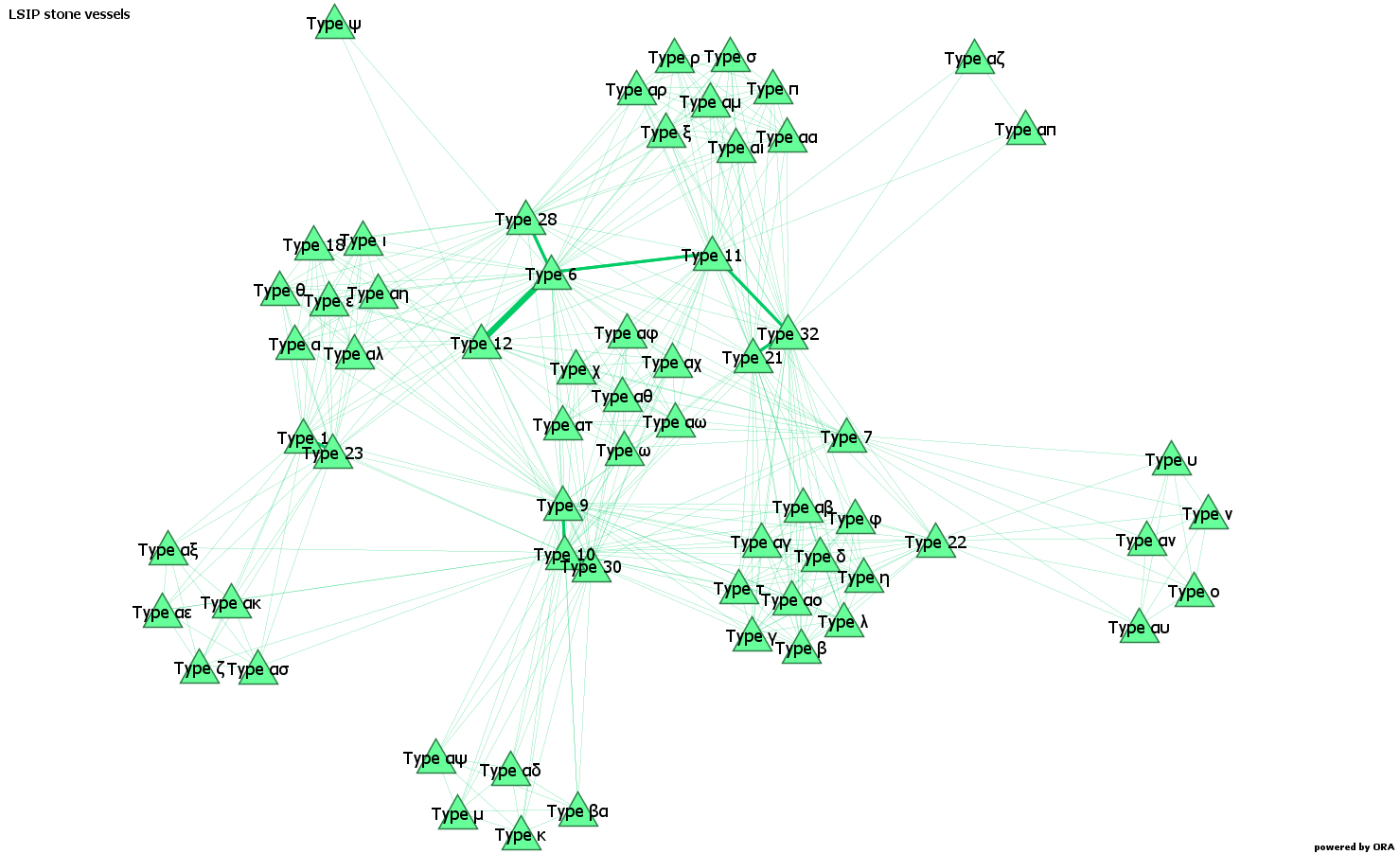
These two one-mode networks are weighted, because the links are based on the amount shared (i.e. stone vessels or sites). Technically, it would be possible to make these networks binary – i.e. to “binarize” them – considering only if sites share a type or not, or if stone vessels are found together at a site or not.
Furthermore, you can consider analysing only one of the two networks or both. It really depends on the questions that you want to answer. In my research, I wanted to study the relationships between the sites and the roles they played in different networks.
Hence, for the one-mode network, where I counted how many types of vessels sites had in common, I opted for the first weighted network. But if my questions had been different – for example, examining the distribution of particular types of stone vessels or detecting types that are usually found together and whose combination might be a pattern in material culture – I would have opted for the second network.
Direct versus undirected networks
One last point useful to touch upon is the “directed” or “undirected” network. In an undirected network, you don’t consider where the connection starts: you consider it reciprocal and the two elements are equal when it comes to their connection. This is the case, for example, in the first one-mode network displayed here, where it is not shown if the stone vessels travelled from one particular site to another: when two sites share a type of stone vessel, they are believed to be equal.
In a directed network, the links go from one element (i.e. the origin) to another (i.e. the destination). The fact that this is a directed link is represented using arrows in a graph. If, for instance, you know that a site produces a particular type of object, such as vessels of a specific material or shape, this site will be at the start of the link, while the site that receives the object will be at the end of it.
In this case, you can also make it weighted, counting, for example, the types exchanged, or the number of vessels or contexts as explained above. You can also make it binary, considering only if types are shared or not. As in the previous cases, the choice depends on your data and the questions you’re seeking to answer. The graph for a weighted directed network will look like the following. Note that in some instances the arrows go to both sites, but one arrow is smaller than the other. This means that each site exchanges one or more types with the other, but one direction the number of contexts or of specimens, or of types as in the case of the graph, is smaller.
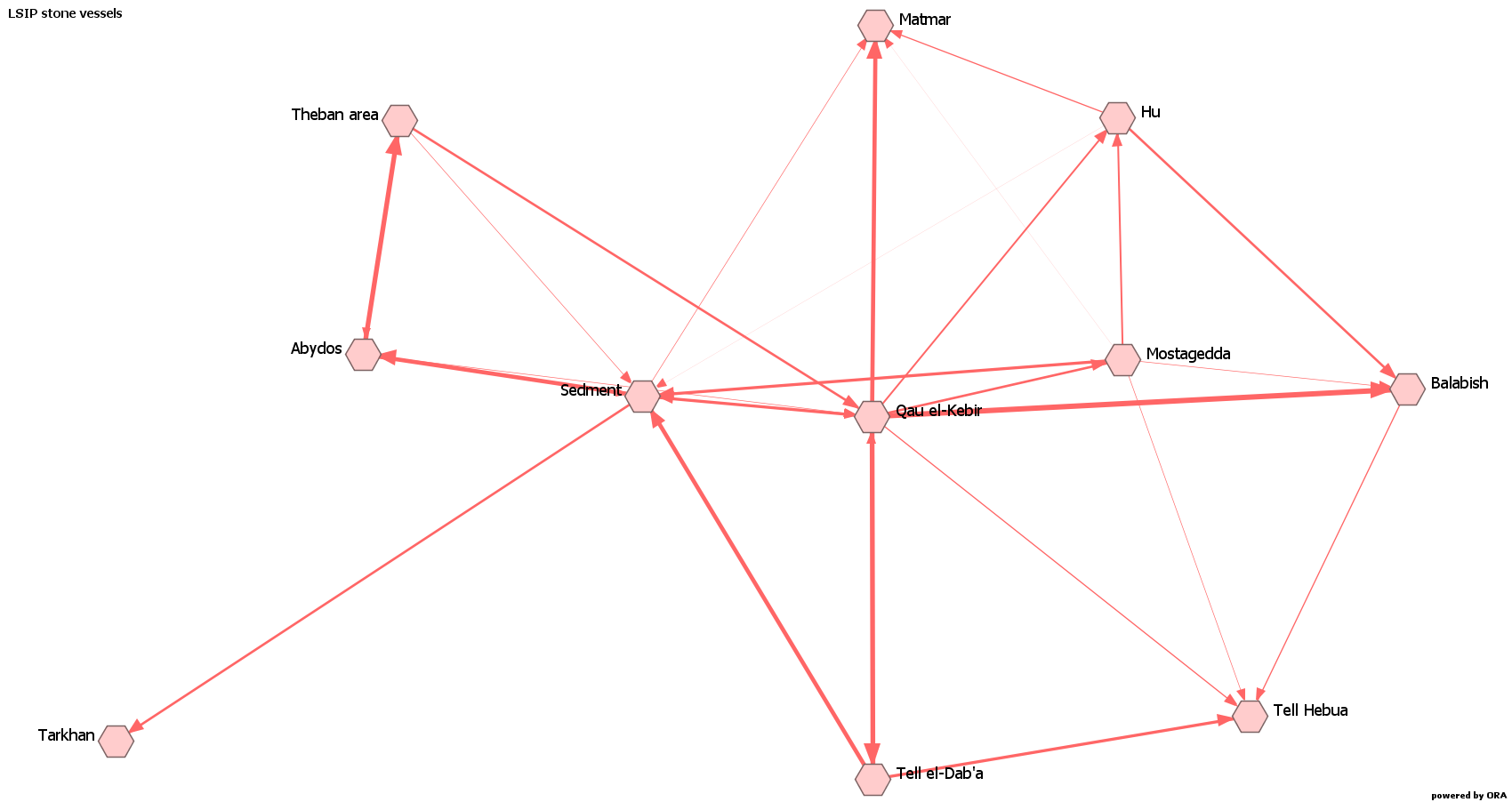
Again, opting for a directed or undirected network depends on your data and your research questions. In my research, I had to opt for an indirect network, because I could not establish where the objects found at a site came from precisely. To go back to the example of the stone vessels, when I found out that two or more sites had a similar type, I could not determine which one of these sites was the origin: in other words, I could not ascertain from which site (if any) the stone vessel in question had been transported.
However, what I could say, was that the sites with similar stone vessels were sharing a similar material culture and that, as a consequence, this suggested that there were contacts between them. This was the premise of my research: the more elements of material culture that are shared between sites, the closer the contacts must have been between them.
Closing remarks
There are many options that you have when it comes to network analysis. I have only illustrated a few basic ones, and I’ll discuss some other, more advanced types of networks in future articles in this series.
The choices you make ultimately depend on your data and your research questions. After dealing with them, and after building your database and your matrix, it is time to “feed” this matrix to the software. In my next article, I will talk about some options for the matrix and for the software, comparing them and sharing what my experience has been with them.
