In the previous article in this series on network analysis in archaeology, I discussed the first one of the main four measures, or mathematical algorithms, used in network analysis: the degree centrality. I have also discussed further algorithms derived from the degree centrality.
In this article, I will discuss the second one of the measures: the betweenness centrality. This measure shows how important the examined entity is as intermediary, a bridge, between other pairs (or even groups) of entities in the network, or an in-between between third parties (if you prefer).
In other words, betweenness centrality detects entities that have the highest capacity of linking other entities in the chains of contacts in a network and that, as a consequence, can have control over the flow and circulation of objects/resources/information/ideas.
The betweenness centrality
In technical terms, the betweenness centrality of an entity measures how often the examined entity is on a geodesic between other entities. A geodesic is the shortest path, or sequence of links, between two entities in a network.
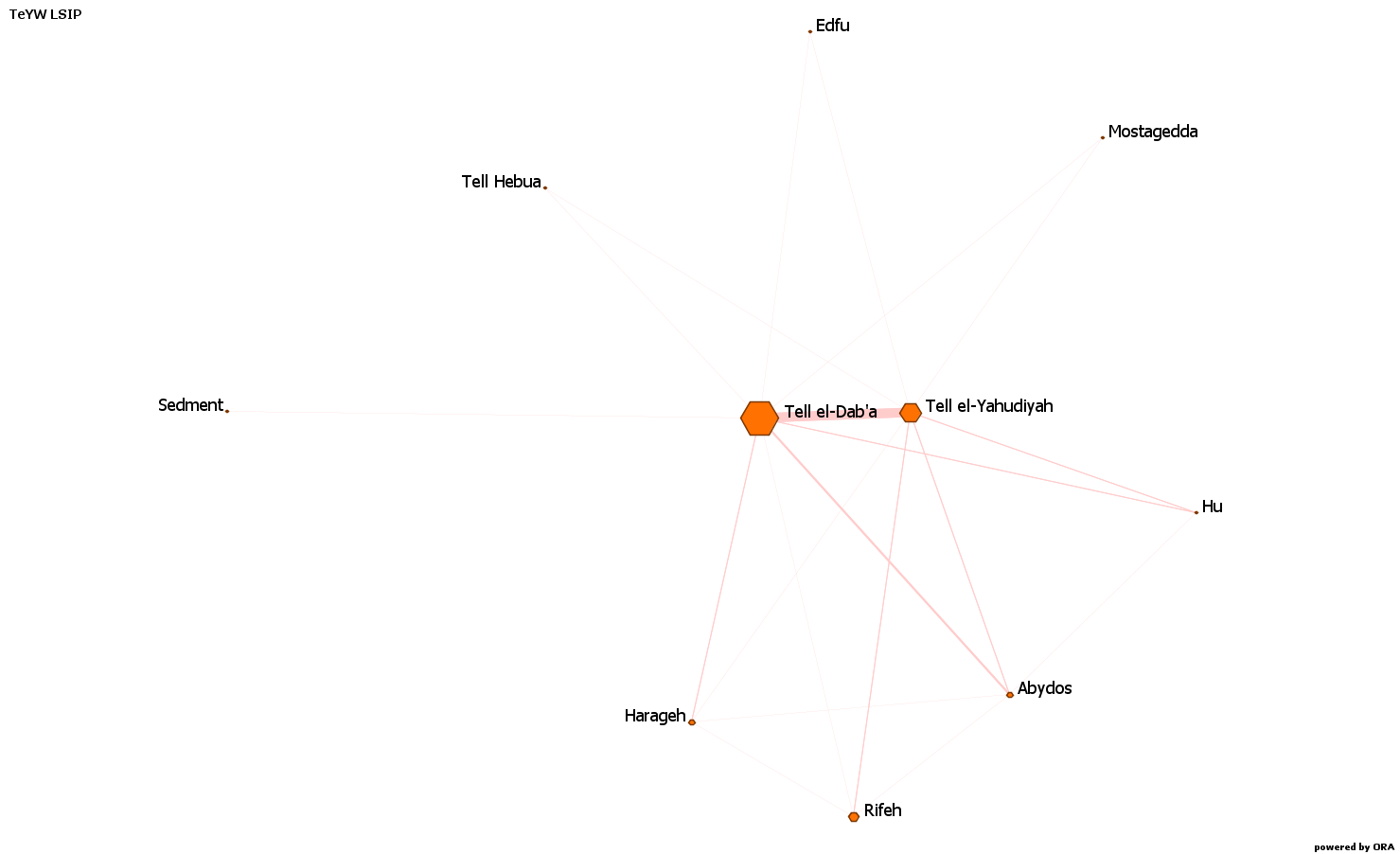
For example, in Figure 1, Edfu and Mostagedda are not directly linked, because they have no types of Tell el-Yahudiyah ware in common, but they are connected through Tell el-Dab’a and Tell el-Yahudiyah, and the latter are also connected between them, because they have types in common.
Therefore, to go from Edfu to Mostagedda (but also vice-versa) the following routes are available:
- Edfu – Tell el-Dab’a – Tell el-Yahudiyah – Mostagedda
- Edfu – Tell el-Dab’a –Mostagedda
- Edfu – Tell el-Yahudiyah – Mostagedda
As you can see, the last two options have fewer steps, therefore they are the geodesics between Edfu and Mostagedda – and yes, you can have more geodesics, and the denser the graph, the more geodesics will be present.
Geodesics
Mathematically, betweenness centrality is based on the proportion of all the geodesics – i.e. shortest paths – between two nodes that the geodesics that include the examined entity; this can be referred to as partial betweenness. The partial betweenness can be calculated with the following formula:
$$b_{ijm} = \frac{g_{ijm}}{g_{jm}}$$
Here, \(g_{ijm}\) represents the number of geodesics between \(j\) and \(m\) containing \(j\) (the entity examined), while \(g_{jm}\) represents the number of geodesics connecting \(j\) to \(m\). From this, is possible to calculate the betweenness centrality:
$$C_{B(i)}= \sum_{j}^{n} \sum_{m}^{n} b_{ijm} \quad (i \ne j, i \ne m)$$
This is summing the results given by calculating the partial betweenness of the examined entity, \(i\), for each pair of nodes, represented by \(j\) and \(m\).
Going back to Figure 1, if you want to know the betweenness centrality of Tell el-Dab’a, first you take each pair of the other sites (e.g. Harageh and Abydos, Rifeh and Sedment, Hu and Abydos, and so on), and you calculate the ratio between the geodesic that pass by Tell el-Dab’a and the geodesics that do not. Then, you sum up the calculated ratios.
In a weighted network, such as the one in Figure 1, both undirected and directed, this measure is also based on the weight of the links, following the assumption that more similarities forming a link mean more contacts and, thus, a lower cost to maintain them. You can also calculate the measures for edges, but I will write about that in a future article.
Central points
In a graph, the most central point is the one in the middle of a star. Mathematically, the centrality of this point corresponds to the following formula, referred to as maximum betweenness centrality:
$$maxC_B = \frac{n^2-3n+2}{2}$$
Where \(n\) represents the number of nodes in a graph. Therefore, this formula can calculate the highest betweenness centrality possible in a network, namely value of the most central point in a graph.
From this, you can calculate relative betweenness centrality of an entity, by dividing the double of its betweenness centrality by the maximum betweenness centrality in the same network.
The formula is as follows:
$$C’_{B(i)} = \frac{2C_{B(i)}}{n^2-3n+2}$$
This is the ratio between the betweenness centrality of an entity and the numerator of the maximum betweenness; you need to double the betweenness centrality because the maximum betweenness is not halved (therefore is double than in the previous formula).
At this point, it can seem apparent that the betweenness centrality, while examining the role of each single entity in the network, takes into account the entire structure of the network and it is based on its position in the network.
Network measures
in the previous article, I mentioned that there are centrality measures, concerning the single entities, and network measures, concerning the structure of the entire network.
A network measure that can be calculated from the betweenness centrality is the betweenness centralization, which is given by dividing the sum of the variations of the betweenness centrality scores of all the entities of a network, by the maximum variation in betweenness centrality scores in the same network.
It is given by the formula:
$$C_{B()} = \frac{\sum_i^n(C’_{B(*)} – C’_{B(i)})}{Max(\sum_{i}^{n}(C’_{B(*)} - C’_{B(i)})}$$
\(C’_{B(*)}\) is the betweenness centrality of the network’s most central vertex, and \(C’_{B(i)}\) is the betweenness centrality of any other entity in the network. Basically, you take the point with the highest betweenness, calculate the difference between this and the betweenness centrality of each other entity in the network, you sum all the differences, and you divide this by the maximum difference detected. This is useful if you want to control the entire graph and get a general idea of its structure.
Applying network measures
What does this measure mean, when applied to archaeological material? In the case of my research, the betweenness centrality was determined by how often a site was the find place of (types of) objects that create connections between other sites. Therefore, this measure would put focus for instance on a site which features objects of multiple types that are found separately at other sites, or on a site which features a particular common type, namely a type widely found at the sites.
Because of the fact that my data did not allow me to take directions into account, I could not say where the objects were coming from and where they were going. However, places with a high betweenness centrality funnelled the connections in the network and bring the material culture of other sites together. Therefore, one possibility is that such places could be interpreted as places of exchange or (re)distribution centres for these objects.
A few words about something that surprised me when I started my project: it is common to have a big difference between the entities you examine, when it comes to network analysis, as you can see in Figure 1. Therefore, be prepared to see that in your analysis a few entities have a high betweenness centrality, while most of the others have a very low one.
Because of its nature, betweenness centrality detects what in my opinion can be compared to neuralgic centre(s) of the network, points that are vital in maintaining the connections by ensuring that the flow continues from one point to the other. Of course how many vital points there are depends on the kind of network, but more often they will not be many.
The main problem is that betweenness centrality considers only geodesic paths, in other words it assumes that whatever flows through the network travels only along the shortest possible paths, in the most efficient way. However, reality is more nuanced and paths, and geodesic paths, are only one of the possible ways that something can move in a network. I will talk more about this in a future article, after discussing all the main measures.
For now, suffice to say that there are multiple ways in which anything can circulate in a group, counting if it spreads only form one or multiple entities, if goes to one or more entities at the same time, and if it passes one or multiple times through the entities and the connections of the network.
Moreover, it appears that betweenness centrality is more prone to Type I errors (“false positives”), therefore leading to overestimations. Nevertheless, it has been shown to be useful to understand network changes and, when examining the flow in a network, the frequency of passage, and to be less sensitive to Type II errors (“false negatives”, which lead to under-estimation).
The density of a network
One measure that can in some cases influence the betweenness centrality is the density of a network. This is the proportion between the links that are actually present in the network and the maximum number of links that the same network could possess.
When the density is at its maximum, the network is called complete: each node is connected to all the other nodes of the network. This measure reveals the general connectedness of a network, but it depends on the size of the network, so that it is less useful when comparing networks of different sizes.
It is given by the following formula:
$$d(G)^u=\frac{m}{\frac{n(n-1)}{2}}=m \times \frac{2}{n(n-1)}=\frac{2m}{n(n-1)}$$
Here, \(m\) is the number of edges and \(n\) is the number of nodes in a network.
Closing remarks
Despite being heavy on the mathematics, I hope this article gives you an idea of how you can use the measures discusses. Should you be using it? As always, it depends on your data, your questions, and the kind of network you are analysing.
Betweenness centrality gives the idea of a flow passing through specific points where a specific route on a number of times. If your data allow for an approximation of this model, then you can consider using it. You should always bear in mind that studying networks is making an ideal model to explain real-life phenomena.
Therefore, if what you are studying can be idealized as a network, with flow and circulation of ideas/knowledge/information/objects/resources, then it is most useful. Moreover, each measure has some assumptions about how the flow happens, as I mentioned earlier about geodesic paths. If this assumption is applicable to what you are studying, then also the measure will be informative for you.
Further reading
- J.M. Bolland, “Sorting out centrality. An analysis of the performance of four centrality models in real and simulated networks”, Social Networks 10 (1988), pp. 233-253.
- S.P. Borgatti, “Centrality and network flow”, Social Networks 27 (2005), pp. 55-71.
- L.C. Freeman, “A Set of Measures of Centrality Based on Betweenness”, Sociometry 40 (1) (1977), pp. 35-41.
- L.C. Freeman, “Centrality in social networks. Conceptual clarification”, Social Networks 1 (1979), pp. 215-239.
- L.C. Freeman, S.P. Borgatti, and D.R. White, “Centrality in valued graphs: A measure of betweenness based on network flow”, Social Networks 13 (1991), pp. 141-154.
- J. Scott, Social Network Analysis (fourth edition, 2017).
- D.R. White and S.P. Borgatti, “Betweenness centrality measures for directed graphs”, Social Networks 16 (1994), pp. 335-346.
The mathematical formulae are formatted in LaTeX and are rendered on this page using MathJax, a JavaScript display engine.
