In the last two articles in this series, I have discussed two of the centrality measures used in network analysis. I have shown how you can calculate and interpret the degree centrality and the betweenness centrality, as well as other algorithms based on them.
Here, I will focus on the closeness centrality, which is the third one of the centrality measures. It indicates how important an entity is, based on how well indirectly connected it is to other entities.
Closeness centrality
What does this mean? If you look at the figure below, which is based on the types of scarabs and seals in common between the Egyptian sites during the Late Second Intermediate Period, you will see that Tell el-Retaba is among the nodes with the smallest number of links (only 6, while the highest number of connection established by a node in the same network is 14) and with the weakest links (each link is only made of one type in common).
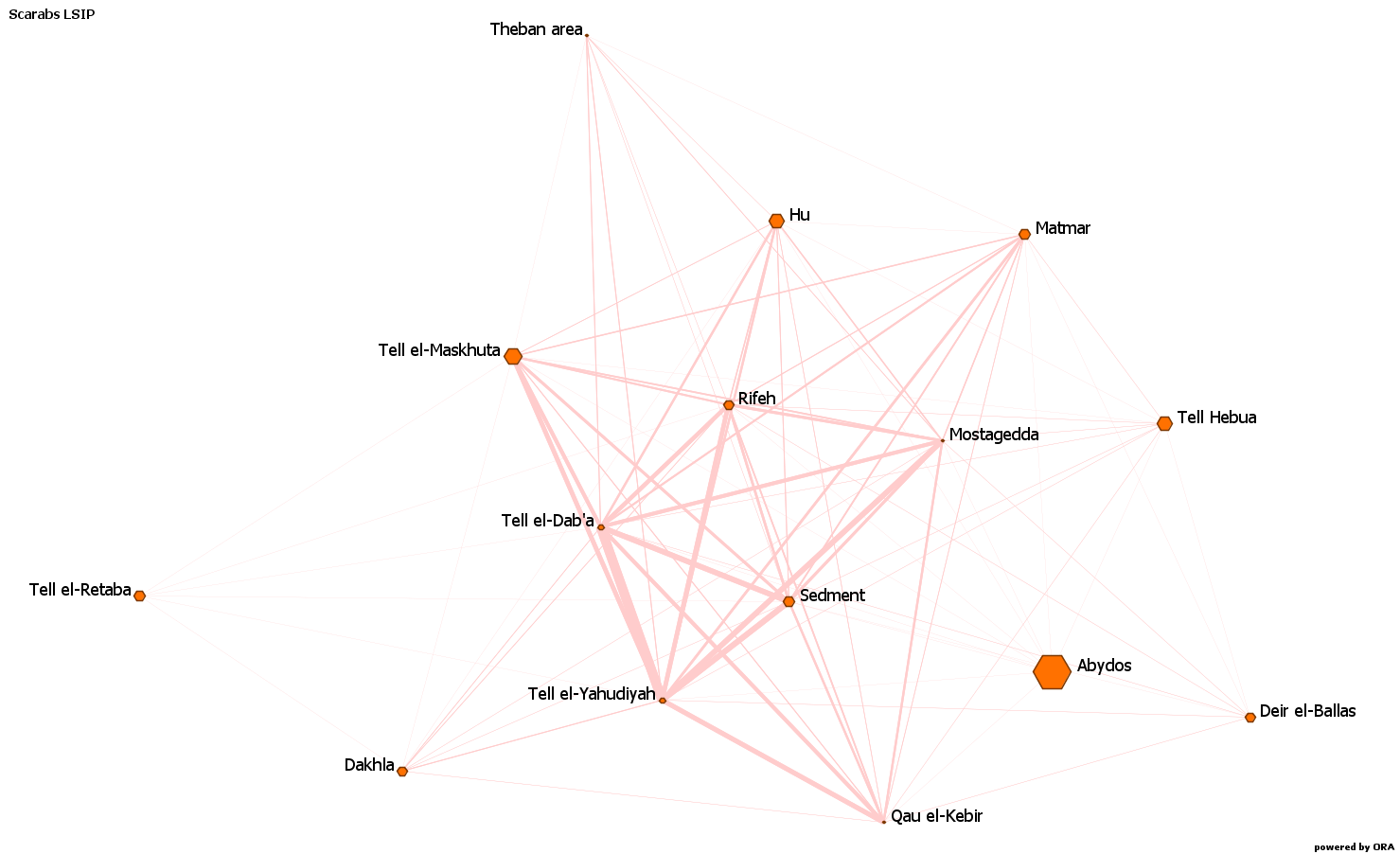
At the same, time, it is not among the sites with the power to link other sites, as you can notice if you look closely at the graph and make the mathematical calculations. Therefore, when it comes to direct connections, or to its importance as a linking element, Tell el-Retaba is not one of the major sites, therefore is not a central node: that is why it is also on the edge of the graph.
However, it is not more than one step away from other entities. This means that, if you trace the links and look for the shortest paths, it can reach all entities through only one intermediary. In its turn, this means that Tell el-Retaba can not only reach, but can also be easily reached by other entities.
Note that, so far, I’ve been using the word “path” with no particular meaning, but to indicate the chain of connections that links one entity of a network to another. However, technically speaking, “path” means a precise way of transmission/circulation/spreading. I will write an article about these different ways. For now, interpret the term “path” as neutral.
From the mathematical point of view, the closeness centrality can be calculated using the following formula:
$$C_{C(i)} = N\frac{1}{\sum_{i}^{n}d_{ij}}$$
This means that if you want to know the centrality of an entity (\(i\)), first you calculate all the shortest paths between this entity and the others (\(d_{ij}\)), sort of as we did earlier with Tell el-Retaba. Then, you sum these results (\(\sum_{i}^{n}d_{ij}\)).
Afterwards, you divide 1 by this sum, so that the smallest number – i.e. the entity with the shortest paths – comes on top and has the highest value. Given that the result is a very small number, to make it more significant, you multiply it by the number of nodes (\(N\)) that form the network.
To sum up, the fewer steps you need to take between an entity and the others, the higher the closeness centrality is, and the easier the entity can reach/be reached. You can also think about the closeness centrality as an estimated time of arrival: if an entity has a higher closeness centrality it means that the time of arrival from (or to) the other points is generally lower that the one of other entities.
Complicating matters
In the example shown here, with an undirected network, it there is no difference between reaching and be reached. However, if your network is directed, you will have to take the directions into account to establish how easily an entity can reach others (also known as radiality) and how easily it can be reached (also known as integration). There could be quite some difference between radiality and integration.
For the radiality, you will have to take into account the outbound directions, i.e. the directions going away from the entity you are studying. For the integration you have to take into account the inbound directions, i.e. going towards the entity you are studying.
If you are interested in the structure of the network and in how evenly the closeness centrality is distributed among the nodes, you can calculate the closeness centralization. This is obtained by dividing the sum of the variations of the closeness centrality scores of all the entities of a network by the maximum variation in closeness centrality scores in the same network.
The mathematical formula is as follows:
$$C_{C()} = \frac{\sum_i^n(C’_{C(*)} – C’_{C(i)})}{Max(\sum_{i}^{n}(C’_{C(*)} - C’_{C(i)})}$$
\(C’_{C(*)}\) is the entity with the highest closeness centrality in the network, and \(C’_{C(i)}\) is the closeness centrality of any other entity in the network. You take the point with the highest closeness centrality, then you calculate the difference between this and the closeness centrality of each other entity in the network, then you sum all the differences, and at the end you divide this by the maximum difference detected.
Closeness centrality in practice
Practically speaking, what does it mean having a high closeness centrality? If an entity can easily be reached, it could mean that it gets first whatever is circulating, which can be good or bad depending on what is circulating.
Imagine the difference it would make if we were studying the circulation of a virus – we’re unfortunately all too familiar with the COVID-19 pandemic – or the circulation of some gossip, or which facility can be best reached using metro lines.
In archaeology, it could be about studying the circulation of a new type of object or material attested in the material culture. But also other things can be studied, such as an iconographical motive, a new technique, and so on.
When the entity can easily reach others, it means that it can spread easily whatever it is circulating, even to entities that are not directly connected to it – again quite the difference between a virus or gossip, or a new type of technique or object!
In this respect, the difference between the degree centrality and the closeness centrality is quite evident:
- The first one considers the transmission from an entity to its direct connections, and it shows the spreading or circulating potential of an entity based on the number of direct connections, regardless of its position in the entire network.
- Differently, the closeness centrality takes into account the entire network the entity is a part of, and the position of an entity in its network.
While in directed networks you can differentiate between an entity than can easily being reached, and an entity that can easily reach others, this is not possible in undirected networks.
This was the case also with my networks, which were all undirected. What could I say, then, was that a site with a high closeness centrality was easily in contact with other sites, based on the types of objects in common. I couldn’t determine if a site would be the one disseminating or receiving/adopting/adapting the objects or types.
What I should also mention is that the closeness centrality, in my case, was the least significant of the four measures I used. By now you know all of them, but I will go into more detail about the fourth one – the eigenvector centrality – in my next article.
Because the values were mostly small – something that is already a tendency of this measure, unless you have a large number of entities – and I couldn’t detect significant differences between the sites. However, I noticed that sites that have a higher betweenness centrality tend to have a higher closeness centrality. This derives from the fact that both measures take into consideration the overall structure of the network, from different points of view.
Closing remarks
Now, the usual question: should you use this measure? As I have said when talking about the other measures, it depends on your data and your questions. The closeness centrality appears to be more useful in directed networks and if you focus on entities which are more at the margins of the network.
One important thing to keep in mind is also that, as with the betweenness centrality, the closeness centrality assumes that whatever is circulating or spreading always takes the shortest path. But real life is more complicated, and the path chosen is not always the shortest one.
For example, if you want to reach a museum by bus, you could decide to take two buses instead of an available direct connection, because you prefer the view or you want to avoid some particular neighbourhood, or because this allows your friend to join you on the trip. Moreover, the closeness centrality assumes that an entity knows beforehand what path to follow. However, real life is, again, different.
Despite these drawbacks, I advise that, before dismissing this measure, you experiment and try it, to see if it gives you significant results, or if on the contrary it does not. I also advise, not only with the closeness centrality, but with the other measures, to really think about what you are studying and how it circulates, spreads, is diffused or disseminated.
Again, studying the spread of a virus or how to locate the easiest reachable cinema using the tube is quite different, because they work in different ways, as I will show in a future article – and if and how the closeness centrality would help understanding this circulation, spread, diffusion, dissemination, and so on.
Further reading
- J.M. Bolland, “Sorting out centrality. An analysis of the performance of four centrality models in real and simulated networks”, Social Networks 10 (1988), pp. 233-253
- S.P. Borgatti, “Centrality and network flow”, Social Networks 27 (2005), pp. 55-71.
- L.C. Freeman, “Centrality in social networks. Conceptual clarification”, Social Networks 1 (1979), pp. 215-239.
- J. Scott, Social Network Analysis (fourth edition, 2017).
